Beschreibung bivariater Datensätze I: Abhängigkeitsmaße
Aufgabe 1
Bei einer Verkehrskontrolle wurden 10 Personen erfasst. Für die beiden Merkmale Alter und Alkoholgehalt ergab sich folgende Tabelle:
| \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Alter | 20 | 21 | 20 | 22 | 20 | 22 | 21 | 20 | 21 | 21 |
| Promille | 0.2 | 0.1 | 0.0 | 0.2 | 0.1 | 0.1 | 0.2 | 0.0 | 0.1 | 0.0 |
a) Stellen Sie in einer Kontingenztabelle die absoluten und relativen Häufigkeiten dar.
b) Bestimmen Sie den \(\chi^2\)-Koeffizienten und den normierten Kontingenzkoeffizienten und interpretieren Sie ihr Ergebnis.
c) Wie ändern sich die beiden Koeffizienten, wenn sich der Stichprobemumfang verdoppelt? Ändern eine Umordnung der Spalten und / oder Zeilen das Ergebnis?
Lösung zu Aufgabe 1
a) Kontingenztabelle für absolute und relative Häufigkeiten
| Alter: 20 | Alter: 21 | Alter: 22 | \(\sum\) | |
|---|---|---|---|---|
| Promille: 0.0 | 2 (0,2) | 1 (0,1) | 0 (0,0) | 3 (0,3) |
| Promille: 0.1 | 1 (0,1) | 2 (0,2) | 1 (0,1) | 4 (0,4) |
| Promille: 0.2 | 1 (0,1) | 1 (0,1) | 1 (0,1) | 3 (0,3) |
| \(\sum\) | 4 (0,4) | 4 (0,4) | 2 (0,2) | 10 (1,0) |
b) \(\chi^2\)-Koeffizient und normierter Kontingenzkoeffizient
Der \(\chi^2\)-Koeffizient beträgt:
\[ \chi^2 = \sum^K_{k=1} \sum^L_{l=1} \frac{(n_{k, l} - \tilde{n}_{k,l})^2}{\tilde{n}_{k,l}} \]
wobei \(n_{k, l}\) die beobachteten und \(\tilde{n}_{k,l}\) die erwarteten Häufigkeiten sind.
Die erwarteten Häufigkeiten werden berechnet als:
\[ \tilde{n}_{k,l} = \frac{\text{Summe der Zeile} \times \text{Summe der Spalte}}{\text{Gesamtzahl der Beobachtungen}} \]
Es ergibt sich folgende Tabelle:
| Alter: 20 | Alter: 21 | Alter: 22 | \(\sum\) | |
|---|---|---|---|---|
| Promille: 0.0 | 1,2 | 1,2 | 0,6 | 3 |
| Promille: 0.1 | 1,6 | 1,6 | 0,8 | 4 |
| Promille: 0.2 | 1,2 | 1,2 | 0,6 | 3 |
| \(\sum\) | 4 | 4 | 2 | 10 |
Womit sich der \(\chi^2\)-Koeffizient wie folgt berechnet:
\[\begin{align*} \chi^2 &= \sum^K_{k=1} \sum^L_{l=1} \frac{(n_{k, l} - \tilde{n}_{k,l})^2}{\tilde{n}_{k,l}} \\ \\ &= \frac{(2 - 1,2)^2}{1,2} + ... + \frac{(1 - 0,6)^2}{0,6} = 1,875 \end{align*}\]
Der Kontingenzkoeffizient wird berechnet als:
\[ C = \sqrt{\frac{\chi^2}{\chi^2 + n}} \]
wobei \(n\) die Gesamtzahl der Beobachtungen ist.
Damit ergibt sich für \(C\): \[ C = \sqrt{\frac{\chi^2}{\chi^2 + n}} = \sqrt{\frac{1,875}{1,875 + 10}} \approx 0,3974 \]
Und für den normierten Kontingenzkoeffizient \(C^*\) gilt:
\[ C^* = \frac{C}{\sqrt{\frac{\text{min}\{K,L\} - 1}{\text{min}\{K,L\}}}} = \frac{0,3974}{\sqrt{\frac{2}{3}}} \approx 0,4867 \]
Es gilt \(0 \leq C^* \leq 1\), also liegt eine mittelstarke Abhängigkeit vor. Über die Richtung des Zusammenhangs lässt sich keine Aussage treffen.
c) Änderungen bei Verdoppelung des Stichprobenumfangs
Es lässt sich mathematisch herleiten, dass:
\[\begin{align*} \chi^2_{\text{neu}} &= \sum^K_{k=1} \sum^L_{l=1} \frac{(2n_{k, l} - 2\tilde{n}_{k,l})^2}{2\tilde{n}_{k,l}} \\ \\ &= \sum^K_{k=1} \sum^L_{l=1} \frac{2^2(n_{k, l} - \tilde{n}_{k,l})^2}{2\tilde{n}_{k,l}} \\ \\ &= \sum^K_{k=1} \sum^L_{l=1} \frac{4}{2}\frac{(n_{k, l} - \tilde{n}_{k,l})^2}{\tilde{n}_{k,l}} \\ \\ &= 2 \chi^2 \end{align*}\]
Bzw.
\[\begin{align*} C_{\text{neu}} &= \sqrt{\frac{2\chi^2}{2\chi^2 + 2n}}\\ \\ &= \sqrt{\frac{2\chi^2}{2(\chi^2 + n)}}\\ \\ &= C \end{align*}\]
und damit auch
\[\begin{align*} C^*_{\text{neu}} = C^* \\ \end{align*}\]
Bei Verdoppelung des Stichprobenumfangs ändern sich die absoluten Häufigkeiten, aber die relativen Häufigkeiten bleiben unverändert. Eine Umordnung der Spalten und/oder Zeilen ändert das Ergebnis nicht, da beide Koeffizienten invariant ggü. Vertauschung sind.
Aufgabe 2
Gegeben sei nachfolgende Tabelle:
| \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| \(x_i\) | 16 | 19 | 17 | 15 | 20 | 19 | 20 |
| \(y_i\) | 100 | 150 | 120 | 90 | 150 | 140 | 160 |
a) Zeichnen Sie das Streudiagramm
b) Bestimmen Sie den Korrelationskoeffizienten von Bravais-Pearson. Interpretieren Sie Ihr Ergebnis.
Lösung zu Aufgabe 2
a) Streudiagram,
Euer Streudiagramm sollte ungefähr so aussehen: 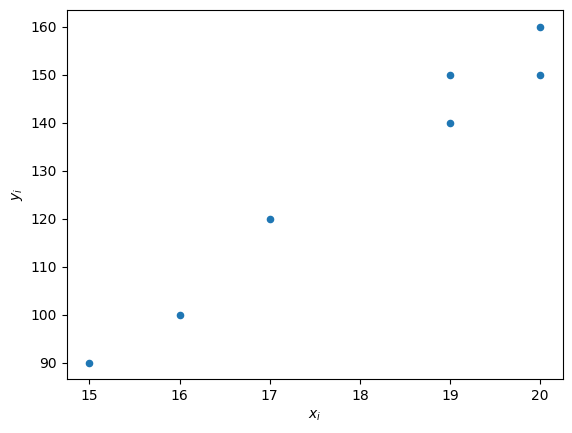
b) Korrelation
Der Bravais-Pearson Korrelationskoeffizient ist
\[ r_{x,y} = \frac{s_{x,y}}{s_x \cdot s_y} \]
Wir benötigen also \(s_{x,y}\) sowie \(s_x\) und \(s_y\), wobei
\[ s_x^2 = \frac{1}{n} \sum^n_{i=1} x_i^2 - \overline{x}^2 \]
bzw.
\[ s_{x,y} = \frac{1}{n} \sum^n_{i=1} x_i y_i - \overline{x} \overline{y} \]
gilt.
Wir berechnen also
\[\begin{align*} \overline{x} &= \frac{1}{n} \sum^n_{i=1} x_i = 18 \\ \\ \overline{y} &= 130 \end{align*}\]
und damit
\[\begin{align*} s_x^2 &= \frac{1}{7} \cdot 2292 - 18^2 \approx 3,4286 \\ \\ s_y^2 &\approx 628,5714 \end{align*}\]
und
\[ s_{x,y} = \frac{1}{7} \cdot 16700 - 18 \cdot 130 \approx 45,7143 \]
um den Korrelationskoeffizienten \(r_{x,y}\) zu berechnen.
\[ r_{x,y} = \frac{s_{x,y}}{s_x \cdot s_y} = \frac{45,7143}{\sqrt{3,4286 \cdot 628,5714}} \approx 0,9847 \]
Für \(r_{x,y}\) gilt \(-1 \leq r_{x,y} \leq 1\). Somit besteht ein sehr starker, positiver und linearer Zusammenhang.
Aufgabe 3
Gegeben sei nachfolgende Tabelle:
| \(i\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(x_i\) | -2 | -1 | 0 | 1 | 2 |
| \(y_i\) | 4 | 1 | 0 | 1 | 4 |
a) Zeichnen Sie das Streudiagramm
b) Bestimmen Sie den Korrelationskoeffizienten von Bravais-Pearson. Nehmen Sie zur Aussage, es bestehe kein Zusammenhang, stellung.
Lösung zu Aufgabe 3
a) Streudiagramm
Euer Streudiagramm sollte ungefähr so aussehen: 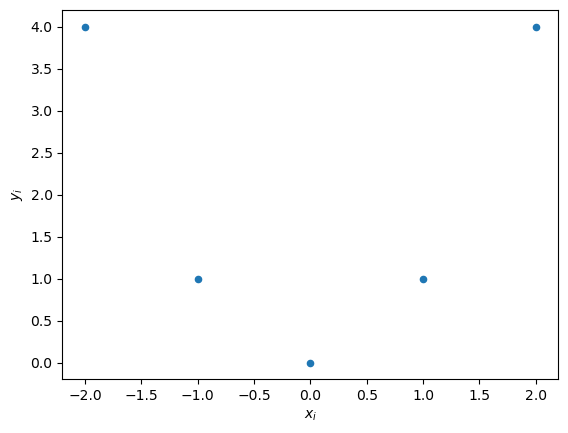
b) Korrelationskoeffizient
Analog zu Aufgabe 2 berechnen wir erneut:
\[ \overline{x}=0; \quad \overline{y}=2; \quad s^2_x = 2; \quad s^2_y = 2,8; \quad s_{x,y} = 0 \]
und damit
\[ r_{x,y} = \frac{s_{x,y}}{s_x \cdot s_y} = \frac{0}{\sqrt{2 \cdot 2,8}} = 0 \]
Die Aussage, es bestehe kein Zusammenhang, ist falsch. Es besteht in diesem Fall ein quadratischer Zusammenhang (\(y = f(x) = x^2\)). Der Korrelationskoeffizient erfasst lediglich lineare Zusammenhänge.
Aufgabe 4
Es wurden sechs Abiturienten befragt, welche Note sie bei ihrer Prüfung erzielt haben:
- (g)ut
- (b)efriedigent
- (a)usreichend
- (m)angelhaft
Zusätzlich wurden sie befragt, ob sie eine vorherige Probeklausur bestanden haben:
- (j)a
- (n)ein
Dabei ergaben sich folgende Antworten:
| \(i\) | Abiklausur | Probeklausur |
|---|---|---|
| 1 | b | n |
| 2 | b | j |
| 3 | b | j |
| 4 | a | n |
| 5 | m | n |
| 6 | g | j |
Kann ein Zusammenhang zwischen der erzielten Note und dem Abschneiden bei der Probeklausur festgestellt werden?
Lösung zu Aufgabe 4
Da die Merkmalsausprägungen lediglich ordinal skaliert sind, sollte hier der Korrelationskoeffizient nach Spearman bestimmt werden. Dafür müssen wir den Antworten einen Rang zuordnen, das Beste bekommt den höchsten Rang. Es ergibt sich:
| \(i\) | Abiklausur (\(x_i\)) | Probeklausur (\(y_i\)) | \(\text{rg}(x_i)\) | \(\text{rg}(y_i)\) |
|---|---|---|---|---|
| 1 | b | n | 4 | 2 |
| 2 | b | j | 4 | 5 |
| 3 | b | j | 4 | 5 |
| 4 | a | n | 2 | 2 |
| 5 | m | n | 1 | 2 |
| 6 | g | j | 6 | 5 |
Der Korrelationskoeffizienten nach Spearman ist:
\[ r_{x,y}^{\text{Spear}} = \frac{s_{rg(x), \, rg(y)}}{s_{rg(x)} \cdot s_{rg(y)}} \]
Daher berechnen wir zunächst \(s^2_{rg(x)}\) und \(s^2_{rg(y)}\) sowie \(s_{rg(x), \, rg(y)}\).
\[\begin{align*} \overline{\text{rg}(x)} &= 3,5 \\ \\ \overline{\text{rg}(y)} &= 3,5 \end{align*}\]
und damit
\[\begin{align*} s^2_{rg(x)} &= \frac{31}{12} \\ \\ s^2_{rg(y)} &= 2,25 \end{align*}\]
und
\[\begin{align*} s_{rg(x), \, rg(y)} &= \frac{1}{6} \cdot (4 \cdot 2 + ... + 6 \cdot 5) - 3,5 \cdot 3,5 \\ \\ &= \frac{1}{6} \cdot 84 - 3,5^2 = 1,75 \end{align*}\]
um den Korrelationskoeffizienten \(r_{x,y}\) zu berechnen:
\[ r_{x,y}^{\text{Spear}} = \frac{1,75}{\sqrt{\frac{31}{12} \cdot 2,25}} \approx 0,7259 \]
Für den Korrelationskoeffizienten nach Spearman gilt \(-1 \leq r_{x,y}^{\text{Spear}} \leq 1\). Somit besteht ein gleichgerichteter, monotoner Zusammenhang.