Beschreibung bivariater Datensätze II: Das lineare Regressionsmodell

Aufgabe 1

In einem Schwellenland wurde eine Studie zum Zusammenhang zwischen Einkommen der Eltern und dem Geburtsgewicht des Kindes durchgeführt. Dabei wurde das monatliche Einkommen \(x_i\) in 1000 GE und das Geburtsgewicht des Kindes \(y_i\) in Pfund betrachtet:

\(i\)	1	2	3	4	5	6	7	8
Einkommen \(x_i\)	2,7	1,9	3,1	3,9	4,0	3,4	2,1	2,9
Gewicht \(y_i\)	5	6	9	8	7	6	7	8

a) Stellen Sie eine sinnvolle Regressionsbeziehung auf

b) Zeichnen Sie das dazugehörige Streudiagramm

c) Bestimmen Sie die Regressionsgerade

d) Das Einkommen einer Familie beträgt 3000 GE. Welches Gewicht wird dann prognostiziert?

e) Ist die gewählte Regression geeignet? Nutzen Sie das Bestimmtheitsmaß für Ihre Stellungnahme.

Lösung zu Aufgabe 1

a) Regressionsbeziehung

Eine sinnvolle Beziehung betrachtet das Gewicht als abhängige und das Einkommen als unabhängige Variable, womit gilt:

\[ y_i = a + b \cdot x_i + \varepsilon_i \]

b) Streudiagramm

Euer Streudiagramm sollte ungefähr so aussehen, hier mit eine Trendlinie: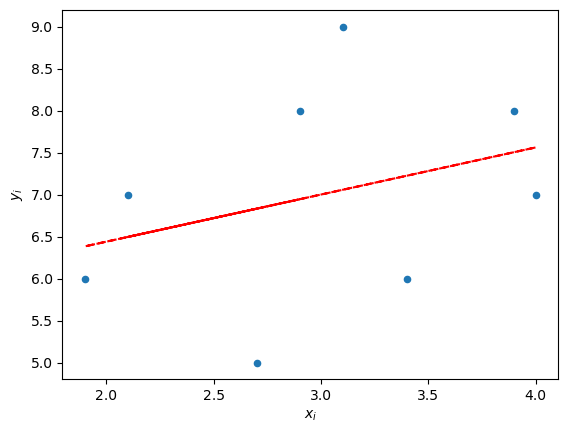

b) Regressionsgerade

Wir wollen nun die Regressionskoeffizienten \(a\) und \(b\) aus der Regressionsbeziehung \[ y_i = a + b \cdot x_i + \varepsilon_i \] schätzen.

Für die OLS Schätzer gilt:

\[\begin{align*} \hat{b} &= \frac{s_{x,y}}{s^2_x} \\ \\ \hat{a} &= \overline{y} - \hat{b} \cdot \overline{x} \end{align*}\]

Wir müssen also voerst die benötigten Werte bestimmen: \[ \overline{x} = 3; \quad \overline{y} = 7; s^2_x = 0,5125; \quad s_{x,y} = 0,2875 \]

Und wir erhalten somit:

\[\begin{align*} \hat{b} &= \frac{s_{x,y}}{s^2_x} = \frac{0,2875}{0,5125} \approx 0,5610 \\ \\ \hat{a} &= \overline{y} - \hat{b} \cdot \overline{x} = 7 - 0,5610 \cdot 3 = 5,317 \end{align*}\]

Als Regressionsgerade ergibt sich dann \(\hat{y} = 5,317 + 0,5610 \cdot x\).

d) Prognose

Einsetzen von \(x=3\) die Gerade \(\hat{y} = 5,317 + 0,5610 \cdot x\) ergibt:

\[ 5,317 + 0,5610 \cdot 3 = 7 \]

Zu erwarten ist also ein Gewicht von 7 Pfund.

e) Bestimmtheitsmaß

Es gilt:

\[ R^2 = \frac{\hat{b}^2 \cdot s^2_x}{s^2_y} = \frac{0,5610^2 \cdot 0,5125}{1,5} \approx 0,1075 \]

Das bedeutet, es werden nur 10,75 % der Variation im Gewicht der Kinder durch das Einkommen der Eltern erklärt. Die Regression ist also eher ungeeignet.

Aufgabe 2

Gegegeben sei folgende Regressionsgerade:

\[ \widehat{\text{schlaf}} = 3586,4 - 0,151 \cdot \text{arbeit} \]

Dabei ist \(\text{schlaf}\) die Zeit in Minuten, die pro Woche zum Schlafen genutzt wird. Die Variable \(\text{arbeit}\) gibt die Minuten an, die pro Woche gearbeitet werden, an.

a) Interpretieren Sie den Achsenabschnitt.

b) Angenommen \(\text{arbeit}\) steigt um 2 Stunden. Wie wirkt sicjh diese Erhöhung auf \(\text{schlaf}\) aus? Handelt es sich um einen großen Effekt?

Lösung zu Aufgabe 2

a) Achsenabschnitt

Der Achsenabschnitt gibt die Schlafenszeit pro Woche in Minuten für jemanden, der überhaupt nicht arbeitet, an. \(3586,4\) Minuten entsprechen ungefähr \(8,54\) Stunden Schlaf pro Tag. Eine durchaus realistische Größe.

b) Effekt von \(\text{arbeit}\)

Die zwei Stunden entsprechen 120 Minuten pro Woche mehr Arbeit. Die Regressionsbeziehung \(\widehat{\text{schlaf}} = 3586,4 - 0,151 \cdot \text{arbeit}\) zeigt, dass sich die Variable \(\text{schlaf}\) dabei um den Wert \(- 0,151 \cdot 120 = -18,12\) reduzieren würde. Das entspricht ca. \(18,12\) Minuten pro Woche weniger Schlaf. Das entspricht \(2,59\) Minuten weniger Schlaf pro Tag, der Effekt ist nicht sonderlich groß.

Ausgabe 3

Gegeben sei folgende Tabelle:

\(i\)	1958	1959	1960	1961	1962	1963	1964	1965	1966	1967	1968	1969
\(P\)	11	9	12	13	14	16	17	30	28	28	42	55
\(Q\)	67	55	56	58	51	57	46	38	39	69	36	35

Dabei ist \(P\) der beobachtete Preis und \(Q\) die nachgefragte Menge eines Gutes in den USA zwischen den Jahren 1958 und 1969.

a) Bestimmen Sie die dazugehörige Regressionsgerade und unterstellen Sie, dass \(P\) der Regressor ist. Interpretieren Sie außerdem die Parameter der Regressionsgerade.

b) Führen Sie eine \(\log\)-\(\log\) Regression durch. Interpretieren Sie außerdem dem Steigungsparameter der Regressionsgerade.

Lösung Aufgabe 3

a) Regression

Da \(P\) der Regressor ist, sei \(x=P\) und \(y=Q\). Wir berechnen die nötigen Größen, um die Parameter \(a\) und \(b\) unser Regressionsgerade \(y_i = a + b \cdot x_i + \varepsilon_i\) zu schätzen:

\[ \overline{x} \approx 22,9167; \quad \overline{y} \approx 50,5833; \quad s^2_x = 184,2415; \quad s_{x,y} \approx -103,6190 \]

Damit erhalten wir als Schätzung für \(b\): \[ \hat{b} = \frac{s_{x,y}}{s^2_x} = \frac{-103,6190}{184,2415} \approx -0,5624 \]

Damit können wir nun auch den Parameter \(a\) schätzen:

\[ \hat{a} = \overline{y} - \hat{b} \cdot \overline{x} = 50,5833 - (-0,5624) \cdot 22,9167 \approx 63,4717 \]

Somit ergibt sich als Regressionsgerade:

\[ \hat{y} = 63,4717 - 0,5624 \cdot x \]

bzw.:

\[ \hat{Q} = 63,4717 - 0,5624 \cdot P \]

Bei einem Preis von \(0\) würde sich demnach die nachgefragte Menge von \(Q=63,4717\) ergeben. Allerdings wird natürlich langfristig kein Unternehmen zu diesem Preis produzieren (\(\text{Gewinn} = Q \cdot P = 0\)). Eine Erhöhung des Preises um eine Einheit würde die nachgefragte Menge um \(0,5624\) Einheiten reduzieren.

Hier sehen wir unsere Regressionsgerade über der Punktewolke: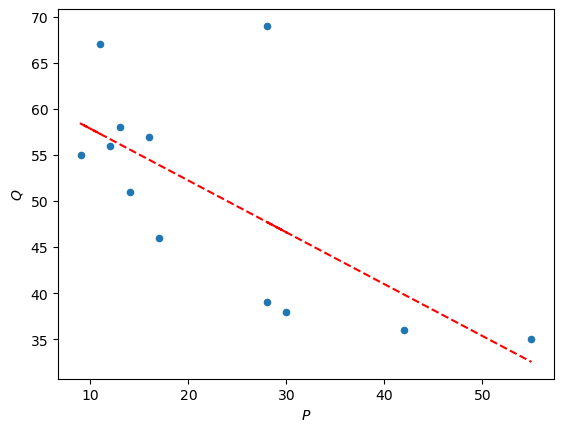

b) \(\text{log}\)-\(\text{log}\) Regression

In einem \(\log\)-\(\log\) Regressionsmodell wird sowohl auf den Regressanden als auch auf den Regressor der natürliche Logarithmus angewendet. Für die logarithmierten Werte ergibt sich:

\(i\)	1958	1959	1960	1961	1962	1963	1964	1965	1966	1967	1968	1969
\(\ln P\)	2.3979	2.1972	2.4849	2.5649	2.6391	2.7726	2.8332	3.4012	3.3322	3.3322	3.7377	4.0073
\(\ln Q\)	4.2047	4.0073	4.0254	4.0604	3.9318	4.0431	3.8286	3.6376	3.6636	4.2341	3.5835	3.5553

Sei \(\ln P = x^*\) und \(\ln Q = y^*\), so ergibt sich: \[ \overline{x}^* \approx 2,9750; \quad \overline{y}^* \approx 3,8980; \quad s^2_{x^*} \approx 0,3006; \quad s_{x^*,y^*} = -0,0908 \]

und damit als Schätzer für die Regressionsgerade:

\[ \hat{b} = \frac{s_{x^*,y^*}}{s^2_{x^*}} = \frac{-0,0908}{0,3006} \approx -0,3021 \]

Damit können wir nun auch den Parameter \(a\) schätzen:

\[ \hat{a} = \overline{y}^* - \hat{b} \cdot \overline{x}^* = 3,8980 - (-0,3021) \cdot 2,9750 \approx 4,7967 \]

Damit erhalten wir als Regressionsgerade:

\[ \hat{y} = 4,7967 - 0,3021 \cdot x \]

bzw.:

\[ \widehat{\ln Q} = 4,7967 - 0,3021 \cdot \ln P \]

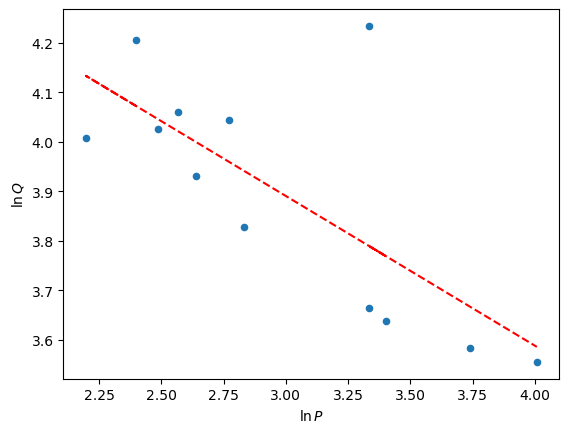
Hier sehen wir unsere Regressionsgerade des \(\text{log}\)-\(\text{log}\) Modells über der \(\text{log}\)-\(\text{log}\) Punktewolke: